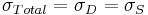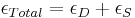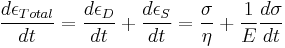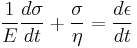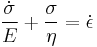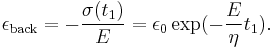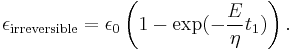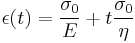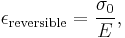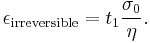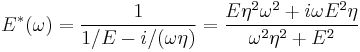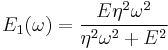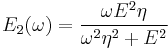Maxwell material

A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.

Contents

Definition

The Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected in series, as shown in the diagram. In this configuration, under an applied axial stress, the total stress, 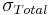{\sigma_{Total}} and the total strain, {\epsilon_{Total}} can be defined as follows:

{\sigma_{Total}}={\sigma_{D}} = {\sigma_{S}}
{\epsilon_{Total}}={\epsilon_{D}}%2B{\epsilon_{S}}

where the subscript D indicates the stress/strain in the damper and the subscript S indicates the stress/strain in the spring. Taking the derivative of strain with respect to time, we obtain:

\frac {d\epsilon_{Total}} {dt} = \frac {d\epsilon_{D}} {dt} %2B \frac {d\epsilon_{S}} {dt} = \frac {\sigma} {\eta} %2B \frac {1} {E} \frac {d\sigma} {dt}

where E is the elastic modulus and η is the material coefficient of viscosity. This model describes the damper as a Newtonian fluid and models the spring with Hooke's law.

If we connect these two elements in parallel, we get a model of Kelvin-Voigt material.

In a Maxwell material, stress σ, strain ε and their rates of change with respect to time t are governed by equations of the form:

\frac {1} {E} \frac {d\sigma} {dt} %2B \frac {\sigma} {\eta} = \frac {d\epsilon} {dt}

or, in dot notation:

\frac {\dot {\sigma}} {E} %2B \frac {\sigma} {\eta}= \dot {\epsilon}

The equation can be applied either to the shear stress or to the uniform tension in a material. In the former case, the viscosity corresponds to that for a Newtonian fluid. In the latter case, it has a slightly different meaning relating stress and rate of strain.

The model is usually applied to the case of small deformations. For the large deformations we should include some geometrical non-linearity. For the simplest way of generalizing the Maxwell model, refer to the Upper Convected Maxwell Model.

Effect of a sudden deformation

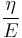If a Maxwell material is suddenly deformed and held to a strain of \epsilon_0, then the stress decays with a characteristic time of \frac{\eta}{E}.

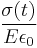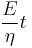The picture shows dependence of dimensionless stress \frac {\sigma(t)} {E\epsilon_0} upon dimensionless time \frac{E}{\eta} t:

If we free the material at time 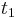t_1, then the elastic element will spring back by the value of

\epsilon_\mathrm{back} = -\frac {\sigma(t_1)} E = \epsilon_0 \exp (-\frac{E}{\eta} t_1).

Since the viscous element would not return to its original length, the irreversible component of deformation can be simplified to the expression below:

\epsilon_\mathrm{irreversible} = \epsilon_0 \left(1- \exp (-\frac{E}{\eta} t_1)\right).

Effect of a sudden stress

If a Maxwell material is suddenly subjected to a stress 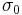\sigma_0, then the elastic element would suddenly deform and the viscous element would deform with a constant rate:

\epsilon(t) = \frac {\sigma_0} E %2B t \frac{\sigma_0} \eta

If at some time 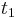t_1 we would release the material, then the deformation of the elastic element would be the spring-back deformation and the deformation of the viscous element would not change:

\epsilon_\mathrm{reversible} = \frac {\sigma_0} E,
\epsilon_\mathrm{irreversible} = t_1 \frac{\sigma_0} \eta.

The Maxwell Model does not exhibit creep since it models strain as linear function of time.

If a small stress is applied for a sufficiently long time, then the irreversible stresses become large. Thus, Maxwell material is a type of liquid.

Dynamic modulus

The complex dynamic modulus of a Maxwell material would be:

E^*(\omega) = \frac 1 {1/E - i/(\omega \eta) } = \frac {E\eta^2 \omega^2 %2Bi \omega E^2\eta} {\omega^2 \eta^2 %2B E^2}

Thus, the components of the dynamic modulus are :

E_1(\omega) = \frac {E\eta^2 \omega^2 } {\eta^2 \omega^2 %2B E^2}

and

E_2(\omega) = \frac {\omega E^2\eta} {\omega^2 \eta^2 %2B E^2}

The picture shows relaxational spectrum for Maxwell material. The relaxation time constant is 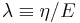\lambda \equiv \eta / E .

Blue curve dimensionless elastic modulus 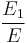\frac {E_1} {E}
Pink curve dimensionless modulus of losses 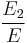\frac {E_2} {E}
Yellow curve dimensionless apparent viscosity 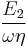\frac {E_2} {\omega \eta}
X-axis dimensionless frequency 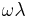{\omega} {\lambda}.

References

See also